Working of a Capacitor

Definition

A capacitor is an electronic device that is used to store electrical energy. They are only used to store the electrons and they are not capable of producing them.

Invention of the Capacitor

There are many stories behind the invention of the capacitor. A German scientist named Ewald Georg von Kleist was known to invent the capacitor in November 1745. But, he did not have any detailed notes or records of his invention. So, he was given the credit for evolution of the capacitor. A few months later a Dutch professor called Pieter van Musschenbroek found a similar device called the Leyden Jar. Scientists approved this to be the first capacitor. After years, both the scientists have been given equal credit for the invention of the capacitor.

Years later, Benjamin Franklin experimented with the Leyden Jar, and was able to make a smaller capacitor which was named as Franklin Square after him. Later English chemist Michael Faraday began experimenting on the Leyden Jar, and invented the first commercial capacitor. This capacitor was made from large oil barrels. This was later progressed in such a way that electric power could be delivered to very large distances.

The Leyden Jar

The Leyden Jar basically consists of a glass jar, which was lined inside and outside with metal foils usually made of lead. The glass jar was half filled with water. The glass jar was used as the dielectric. A brass rod is introduced from the top of the glass jar. A static supply was then given from the brass rod into the jar. When this is delivered the jar will store two equal, but opposite charges in equilibrium which passes on to the ground if a ground wire is given. The figure of a Leyden Jar is given below.

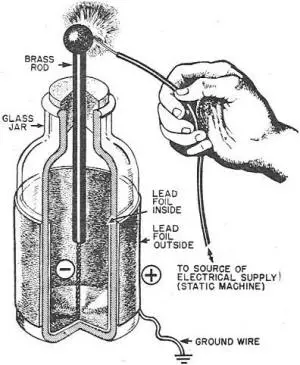
                                                 Leyden Jar

 

Working of a Capacitor

A capacitor consists of two metal plates which are separated by a non-conducting substance or dielectric. Take a look at the figure given below to know about dielectric in a capacitor.

                     

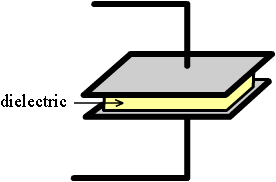
Though any non-conducting substance can be used as a dielectric, practically some special materials like porcelain, mylar, teflon, mica, cellulose and so on. A capacitor is defined by the type of dielecric selected. It also defines the application of the capacitor.
According to the size and type of dielectric used, the capacitor can be used for high-voltage as well as low-voltage applications.
For applications in radio tuning circuits air is commonly used as the dielectric. for applications in timer circuits mylar is used as the dielectric. For high voltage applications glass is normally used. For application in X-ray and MRI machines, ceramic is mostly preferred.
The metal plates are separated by a distance “d”, and a dielectric material is placed in-between the plates.
The dielectric constant of the dielectric material =  e0e………………e0 is the dielectric of air.

The dielectric material is the main substance that helps in storing the electrical energy.

Definition of Capacitance

There are mainly two concepts for defining capacitance. The electrical concept is given below.
Capacitance is said to be the capacitor’s storage potential. In other words, for an existing potential difference  or voltage “V” across the plates, the capacitance is said to be the amount of charge “Q” stored in between the plates.

Capacitance, C = Q/V
Physical concept of capacitance is that capacitance is defined by the physical characteristics of the two plates, such that the capacitance is equal to the ratio between the square area of a plate and the distance between the plates multiplied by the dielectric of the material in between the plates

Capacitance, C = e0e A/d

Working Of A Capacitor – Video

Farad

The capacitance of a capacitor is measured in units called Farads.
A capacitor is said to have 1 Farad of capacitance when the capacitor can hold 1 amp-second of electrons at 1 volt at a rate of electron flow of 1 coulomb of electrons per second. As 1 Farad is a big value, the capacitors are usually denoted in micro farads.

Basic Capacitor Circuits

1. Capacitor connected to a battery

A Capacitor that is connected to a battery is shown below.

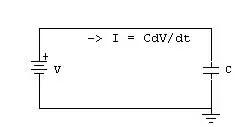
A voltage “V” appears across the capacitor, producing a capacitance “C” and a current “I”. The voltage produced by the battery is accepted by the plate that is connected to the negative of the battery. Similarly, the plate on the capacitor that attaches to the positive terminal of the battery loses electrons to the battery. Thus the capacitor begins charging given by the equation

dq = C*dV, where dQ is the small change in charge and dV is the small change in voltage.
Thus the current can be expressed as
I = C*dV/dt.
When the capacitor is fully charged it will have the same voltage as the battery.

2. Capacitor connected in series

Capacitors C1 and C2 connected in series are shown in the figure below.

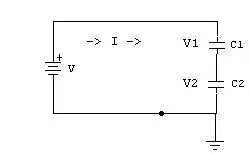
When the capacitors have a series connection the total voltage “V” from the battery is split into V1 and V2 across the capacitors C1 and C2. The overall charge “Q” will be the charge of the total capacitance.
Voltage V = V1 + V2

As in any series circuit the current I is the same throughout

Therefore total capacitance of the circuit, Ctotal = Q/V = Q/(V1 + V2)

This can be further calculated as 1/Ctotal  = 1/C1  +  1/C2

Thus, for a circuit having “n” number of capacitors in series

1/Ctotal  = 1/C1  +  1/C2 + 1/C3 + …… + 1/Cn

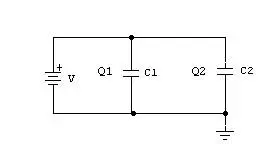
3. Capacitor connected in parallel

As shown in the figure, two capacitorsC1 and C2 are kept in parallel. The voltage across both the capacitors will be the same, “V”. The charge in the capacitor C1 is Q1 and the charge in capacitor C2 is Q2.  Thus we can write the equations as
C1 = Q1/V and C2 = Q2/V.
Total Capacitance, Ctotal = (Q1+Q2)/V = Q1/V  +  Q2/V = C1 + C2

If there are “n” capacitors kept in parallel, then total capacitance can be written as

Ctotal = C1 + C2 + C3 + … + Cn

Advantages

• Since the capacitor can discharge in a fraction of a second, it has a very large advantage. Capacitors are used for appliances which require high speed use like in camera flash and laser techniques.
• Capacitors are used to remove ripples by removing the peaks and filling in the valleys.
• A capacitor allows ac voltage to pass through and blocks dc voltage. This has been used in many electronic applications.